Brief Introduction to Elliptic-curves

1

Ever wanted to understand how Grin works, but the math scared you off? I felt the same. In this 3 part series I’ll take you step-by-step through the process of understanding Mimblewimble once and for all (hint: it’s not as scary as it seems).

This is the 1st part of Introduction to Mimblewimble (It currently sits idly in the new docs, read by almost no-one).

Let’s go. Start fucking reading.

Elliptic Curve Cryptography

Mimblewimble relies entirely on Elliptic-curve cryptography (ECC), an approach to public-key cryptography. Put simply, given an algebraic curve of the form y^2 = x^3 + ax + b, pairs of private and public keys can be derived. Picking a private key and computing its correspnding public key is trivial, but the reverse operation public key -> private key is called the discrete logarithm problem, and is considered to be computationally infeasible.

Let’s review the basics.

Operations

These are the relevant mathematical operations we can do on Elliptic-curve points.

  • Addition - Given two points, we can add them to one another (or subtract) and the result would be a new point on the curve.
  • Multiplication - Given a point, we can multiply it any number of times.

Addition

Given three aligned points P, Q and R, their sum is always 0. We treat this as an inherent property of elliptic curves.

P + Q + R = 0

We can then write it as:

P + Q = -R

So that adding the two points P and Q results in -R, the inverse of R.

If we draw a line passing through P and Q, this line will cross a third point on the curve, R (so that P, Q and R are aligned). If we take the inverse of this point, which is simply the one symmetric to it about the x-axis, we have found the result of adding two curve points, P + Q. Let’s illustrate:

ecc1

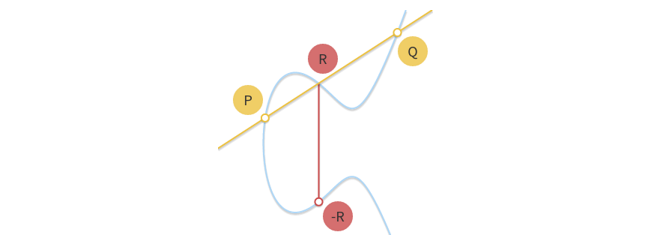
In other words, addition of points is basically hopping around on the curve to a different, seemingly random point; It looks random unless you know the exact operation performed to reach it.

Multiplication

We can’t multiply a point by another point, but we can multiply a point by a number (scalar). Multiplying point P by scalar k would simply require adding point P onto it self k times. This operation is easily demonstrated by assigning k=2 so that k*P = P+P. To illustrate how it would look like on the curve, we draw a tangent line. You can imagine that the line intersects three points, whereas two of them are P, such that:

P + P = -R

ecc2

To calculate 8*P for e.g. wouldn’t take 8 operations, but only 3; you can find 2*P, then add it onto itself, and then add 4*P onto itself, for the final result of 8*P.

Key Pairs

An ECC system defines a publicly known constant curve point called the generator point, G. The generator point is used to compute any public key. A key pair consists of:

  • Private key k – A randomly chosen 256-bit integer (scalar).
  • Public key P – An Elliptic-curve point derived by multiplying generator point G by the private key.

And more clearly, a public key (of private key k) is as follows:

P = k*G

This is easy to compute.

But, if everybody knows points P and G, can they find out what k is? The answer is no; The difficulty of getting from one point to another is precisely the definition of the Elliptic curve discrete logarithm problem.

Note: The specific Elliptic curve that Grin employs is rust-secp256k1 (y^2^ = x^3^ + 7) using Schnorr signature scheme.

Feel free to ask any stupid question, this is a no judgement zone. 2nd part soon.

edit: Simple Introduction to Pedersen Commitments

7 Likes
2

Ok, here my first stupid question. In this example, when using k=8 as privatkey, you say this can be calculated in tree steps by adding P on to itself to get 2P (step 1) then adding it to itself to get 4P (step 2) and then by adding 4P+4P getting to 8P (step 3).

So when using k as a randomly chosen 256-bit integer, are you telling me the same process is used, so using addition in many many steps to reach target of k*P? I thought that CPU’s would have dedicated cirquits nowedays for calculating multiplications even very large once such as a 256 bit large number times P.
Can you tell me if and why the multipliction is still an addition under the hood? Is that because the number is so large or is this just how computers still operate and I wrongly assumed that multiplications could be calculated directly by CPU or GPU.

At least I do understand that finding k would take an immense amount of calculations since basically you have to try all possible vallues of k in k*G to see if they match P (the public key) which is known.

Update: :upside_down_face:so that is the whole trick, the multiplication cannot be done due to the the discrete logarithm problem. Hence using addition the calculation can be done in acceptable time since basically you can grow k*G by 2^n_steps. So k * P can be reached in log2(k) steps (plus a few more). Doing the reverse is apperently not possible.

3

This is beyond my scope but as far as I understand, yes, it’s true that CPUs have their tricks to quickly multiply binary numbers, which includes remembering the results of multiplication between n-bit numbers. Any larger number could be separated into n-bit chunks for quick operations.

However, curve points don’t have the same property; Adding two points results in a seemingly random point on the curve, which you can’t derive quickly using tricks like in binary. It’s indeed the discrete log problem.

4

Thx, I think understanding is appearing in the fog of my mind. The part that my mind conveniently skipped out is that of course P is a point and not number, which is the whole point of EC since points can be added to each-other but not multiplied.
For me it easiest to understand from a programming/process point of view. What gave me initial confusion is the word “adding” since it is basically an iterative process of finding points on the curve by drawing lines between points. From the point of a programmer it is basically an iterative process of jumping from one point on the curve to another by drawing lines between them that intetsect with the curve. Although the process is defined and easy to implement programmatically, the resulting curve point found after each step looks random. As such the resulting point on the curve becomes harder to deduce after each of these iterative steps. For a very large k value (private-key) this becomes impossible to deduce since all possible private-key values (k) have to be tested to see if their output matches public-key P.

Since I think like a programmer, understanding it as a step by step process helps, like shown at the beginning of this video. Thx for writing a clear tutorial. Maybe add a part where you define/say that adding points to one another on the curve is basically hopping around the curve by drawing lines between points.

2 Likes
5

Awesome comment.

  • I’m really glad it clicks for you.
  • You detailing your thinking thinking process is very much appreciated, this is the kind of feedback I’ve been wishing for. I added a paragraph according to your recommendation, let me know if it’s clear enough.

In other words, addition of points is basically hopping around on the curve to a different, seemingly random point; It looks random unless you know the exact operation performed to reach it.

Would this wording be better?

In contrast to addition of regular numbers, adding points is basically hopping around on the curve to a different, seemingly random point; It looks random unless you know the exact operation performed to reach it.

1 Like
6

I like the version you have now best, its direct and simple. It makes it clear that when talking about addition and multiplication we are not talking about the normal math realm but about a procedure specif to the Elliptic Curve.

7

I found this very good explenation of elliptic curve, interactive graphs and it show how multiple points are added to find the point on the curve that matches the public-key*generator-point. In general a very nice site for those who want to understand the inner workings of Bitcoin, really the best I have seen so far.

I was planning to make a Python script to do exactly that, visualize all the curve hopping and how many steps it takes to get to P*G

1 Like